Release curve

The release curve is a supply-management mechanism that governs when and how freshly minted tokens can enter circulation through a protocol-enforced schedule.

It acts as a controlled diffusion of new supply into the market, preventing sudden dilution or disorderly price adjustments. When new assets are tokenized and minted, their corresponding tokens are introduced gradually—not dumped all at once—ensuring smooth market absorption and stable price discovery.

---

Why release curves matter

Without a release curve, all newly minted tokens would hit the market immediately. In Case B (acquisition price below pool price), this can cause:

• Sharp price drops as the pool absorbs instant supply
• Disorderly limit-order execution
• Panic selling as holders react to dilution
• Front-running by sophisticated actors

A release curve turns a supply shock into a supply flow, allowing the AMM to adjust gradually and transparently. By combining time-throttled quotas with price-floor protection, it ensures new supply enters at fair prices—either at current market levels or, when markets dip, via limit orders at acquisition cost that provide natural buy support.

---

One-sentence description

The release curve ensures newly minted tokens flow into the pool gradually — by throttling the rate of release and enforcing that tokens are always sold at or above the acquisition price, either at the current pool price (if above the floor) or via limit orders at the floor price (if the pool trades below it).

---

Key definitions

Term	Symbol	Description	Typical relation
Acquisition price	$p^{\text{acq}}$	Price paid by the issuer for the underlying asset, proven by attestation.	Usually ≤ pool price.
Pool price	$p_{\text{pool}}$	Current mid-price from the AMM; real-time market consensus. This is the market.	Live reference for all trading.
Guarded pool price	$p_{\text{guard}}$	The higher of the live pool price, short TWAP, or RWAP. Used as a safe starting point for new issuance.	$= \max(p_{\text{pool}}, \text{TWAP}_N, \text{RWAP}_Q)$; never below current pool.
Release floor	$p_{\min}(u)$	Minimum price at which tokens can be released at time $u$.	$= \max(p^{\text{acq}}, p_{\text{guard}}(t_0 + u))$; tokens sold at floor if pool below.

---

Formal structure

Let:

• $t_0$: mint time
• $p_t$: current pool price
• $p^{\text{acq}}$: acquisition price
• $\tau$: maximum release horizon
• $r(u) \in [0, 1]$: cumulative fraction of released tokens by time $u$
• $\gamma > 1$: convexity parameter

A convex quantity release curve:

$$r(u) = \left(\frac{u}{\tau}\right)^\gamma$$

At time $u$, the potential supply quota is:

$$m_{\text{quota}}(u) = \alpha m \cdot r(u)$$

where $m$ = total minted tokens and $\alpha \approx 0.8$ = fraction subject to release (with 20% optionally retained by issuer or protocol).

The convex shape releases little early on, letting markets test demand before larger tranches appear.

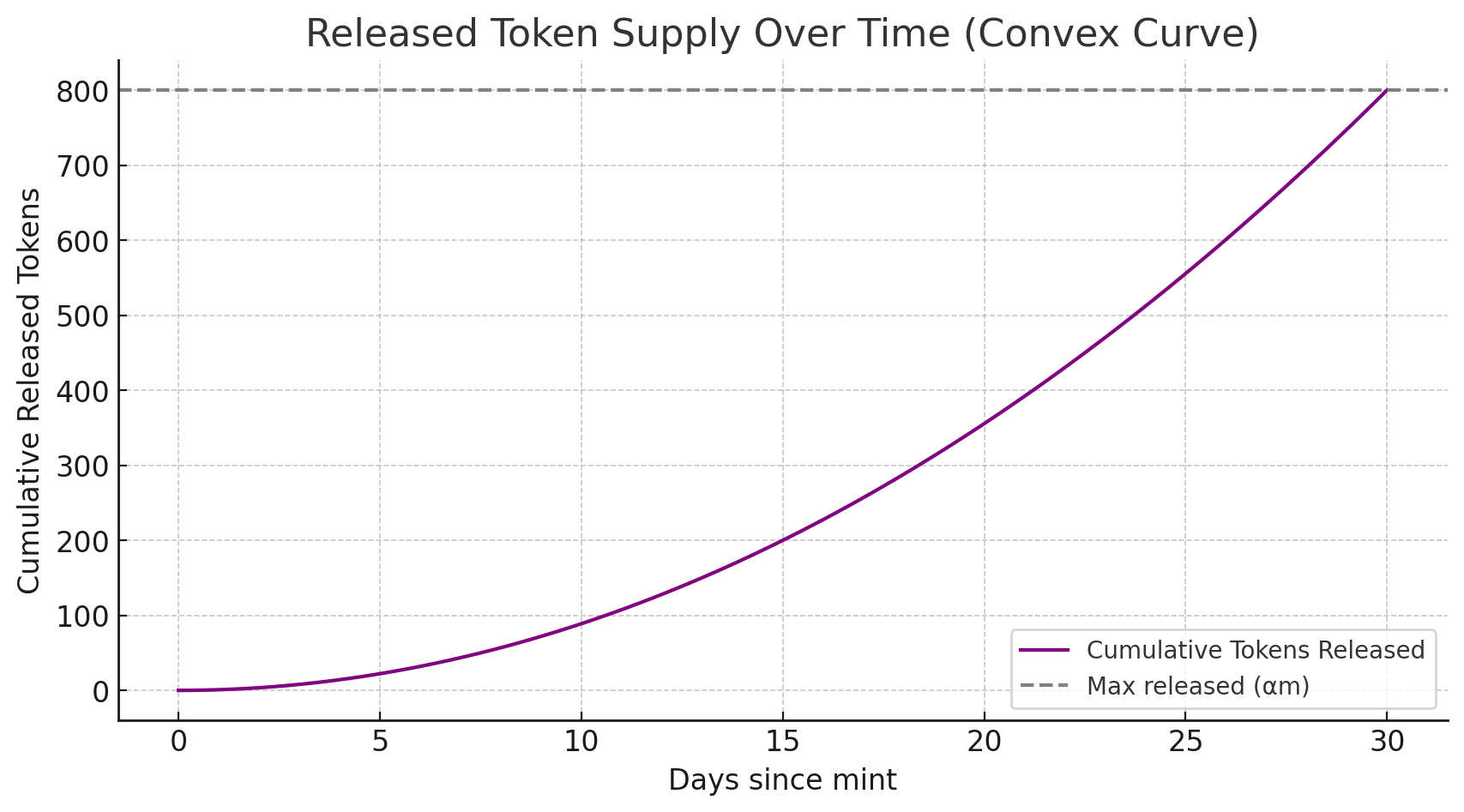
Important: This is a quota (potential supply), not forced release. Tokens enter the pool according to price conditions: at pool price if above floor, or at floor price if below (via limit orders).

---

Release floor: price-aware gate

Quantity release is time-based (defines the quota). The release floor is price-based—it determines the minimum price at which tokens can be sold.

Floor definition

At any time $u$:

$$p_{\min}(u) = \max\big(p^{\text{acq}}, p_{\text{guard}}(t_0 + u)\big)$$

where:

$$p_{\text{guard}}(t) = \max(p_{\text{pool}}(t), \text{TWAP}_N(t), \text{RWAP}_Q(t))$$

Release rule: Tokens from the quota are released as follows:

• If $p_{\text{pool}}(t_0 + u) \geq p_{\min}(u)$: Tokens can be added to the pool at the current pool price
• If $p_{\text{pool}}(t_0 + u) < p_{\min}(u)$: Tokens are still released, but only via limit orders or liquidity provision at the floor price $p_{\min}(u)$

This ensures continuous supply flow while guaranteeing no token ever sells below acquisition cost.

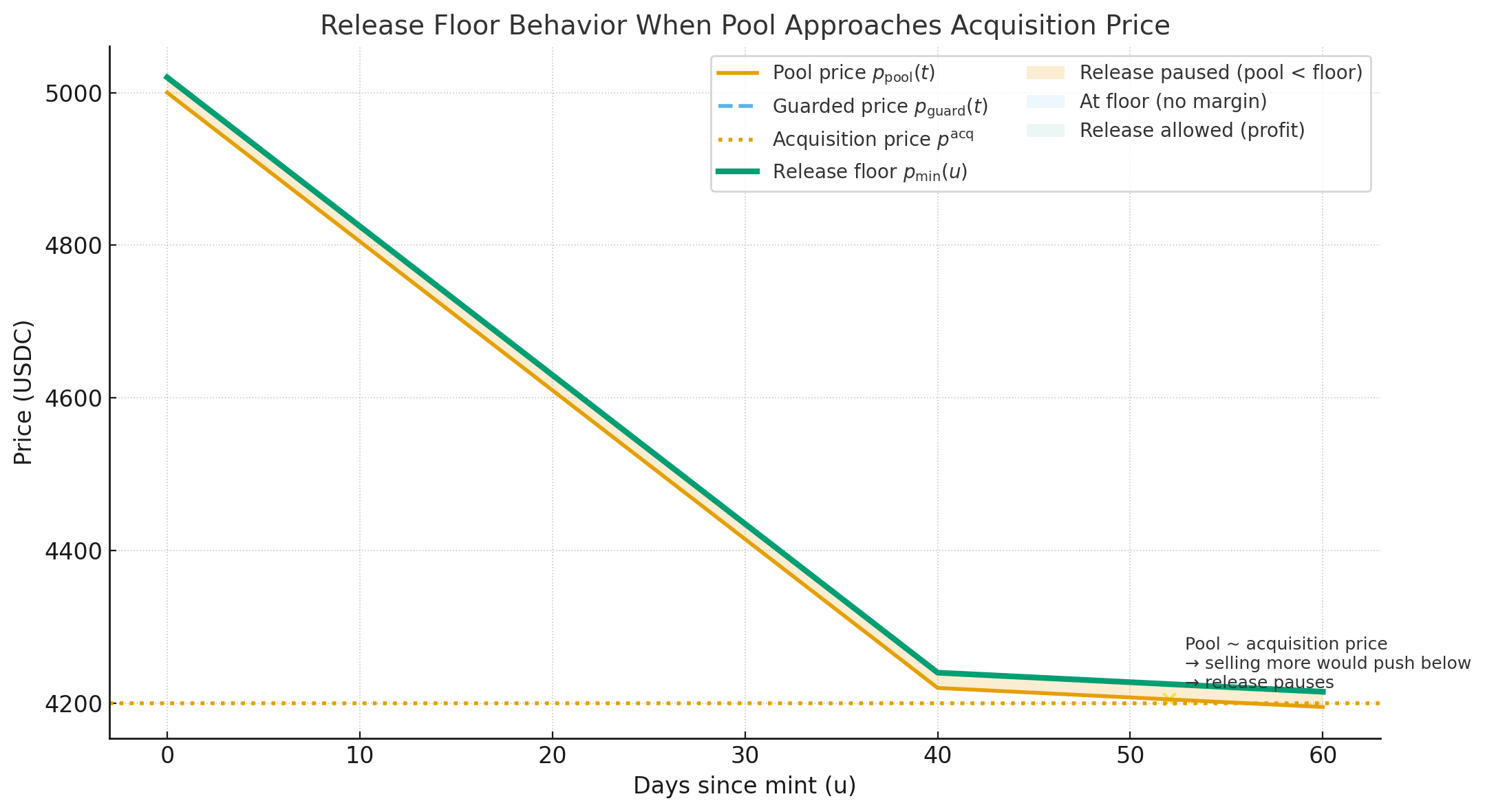
The floor begins at the guarded pool price (e.g., 5,000 USDC) and tracks it as the market evolves—never dropping below it or the acquisition cost. If the pool trades below the floor, tokens continue to release but only at the floor price, either finding buyers or providing liquidity at that level.

---

How the mechanism works

Component	Rule	Purpose
Quantity quota	$m_{\text{quota}}(u) = \alpha m \cdot (u/\tau)^\gamma$	Defines maximum supply that could be released at time $u$.
Release floor	$p_{\min}(u) = \max(p^{\text{acq}}, p_{\text{guard}}(t_0 + u))$	Defines minimum price at which tokens can be sold.
Above-floor release	If $p_{\text{pool}} \geq p_{\min}(u)$	Tokens can be sold at current pool price.
Below-floor release	If $p_{\text{pool}} < p_{\min}(u)$	Tokens released via limit orders at floor price $p_{\min}(u)$.

Phases

1. Hold period – Minted tokens locked; open-interest orders accumulate.
2. Initial release – Small quota available; releases at pool price if above floor, otherwise at floor price.
3. Adaptive release – Quota grows over time; tokens flow at pool or floor price depending on market conditions.
4. Completion – Full quota available after $\tau$ days; market has absorbed supply naturally at fair prices.

---

Worked example

• $p_{\text{pool}} = 5{,}000$ USDC (initial)
• $p^{\text{acq}} = 4{,}200$ USDC
• $m = 1{,}000$ tokens ($\alpha m = 800$ subject to release)
• $\tau = 30$ days, $\gamma = 2$

Quantity quota

Day	$r(u)$	Quota available
7	0.054	43 tokens
15	0.25	200 tokens
30	1.00	800 tokens

Release floor behavior

Assume the guarded pool drifts from 5,000 → 4,800 USDC over 30 days.

$$p_{\min}(u) = \max\big(4{,}200, p_{\text{guard}}(t_0 + u)\big)$$

Day	$p_{\text{guard}}$ (USDC)	$p_{\min}$ (USDC)	Actual release
0	5,000	5,000	None (hold period)
7	4,950	4,950	Up to 43 tokens at pool price (if ≥4,950) or at 4,950
15	4,900	4,900	Up to 200 tokens at pool price (if ≥4,900) or at 4,900
30	4,800	4,800	Up to 800 tokens at pool price (if ≥4,800) or at 4,800

Scenario A: Pool stays at 5,000 USDC → All quotas release at market price.

Scenario B: Pool drops to 4,700 USDC on day 20 → Quota continues to release, but tokens are sold via limit orders at floor price (4,800 USDC), waiting for buyers at that level.

Profit distribution

When tokens sell above acquisition price (e.g., pool at 4,900 USDC vs. acquisition at 4,200 USDC), the surplus is distributed according to the protocol's profit-sharing structure outlined in Coordinated supply management. This aligns incentives by rewarding issuers for acquiring below market, compensating participants (specific distribution strategy to be determined), and funding protocol sustainability.

---

Market impact

Scenario	Behavior
Market overpriced	New supply releases slowly; price drifts down smoothly as liquidity deepens.
Market fair or rising	Quota releases fully; pool absorbs supply at or above acquisition price.
Market drops sharply	Quota continues to release via limit orders at floor price; provides buy support at acq. price.

The mechanism converts abrupt dilution into a market-synchronized supply drip that only flows when demand exists.

---

System invariants

The release curve mechanism maintains a set of always-true conditions that preserve price integrity, fairness, and resistance to dilution shocks. These invariants are enforced on-chain and form the mathematical foundation of the system.

1. Price discipline

$$p_{\text{guard}}(t) = \max(p_{\text{pool}}(t), \text{TWAP}_N(t), \text{RWAP}_Q(t))$$

• The guarded pool price is always $\geq$ current pool price
• Provides a manipulation-resistant live reference for all release logic
• Cannot be gamed by momentary price dips or flash crashes

2. Release floor bound

$$p_{\min}(u) = \max(p^{\text{acq}}, p_{\text{guard}}(t_0 + u))$$

• Newly minted tokens can only enter circulation if $p_{\text{pool}}(t_0 + u) \geq p_{\min}(u)$
• Guarantees no token ever sells below:
  • The issuer's acquisition cost, or
  • The guarded live market price
• Hard lower bound enforced by protocol

3. Supply throttle

$$m_{\text{released}}(u) = \alpha m \left(\frac{u}{\tau}\right)^{\gamma_q}, \quad \gamma_q > 1$$

• Fraction of minted tokens eligible for release grows monotonically and convexly
• $m_{\text{released}}(u)$ never decreases, ensuring deterministic supply growth
• Only the eligible quota increases; actual release depends on price conditions

4. Floor-price protection rule

If the pool price falls below the floor:

$$p_{\text{pool}}(t) < p_{\min}(u) \implies \text{release\_price}(t) = p_{\min}(u)$$

• Tokens continue to release, but only at the floor price (via limit orders or liquidity provision)
• No token ever sells below acquisition cost, even in stressed markets
• Provides natural buy support at the acquisition price level
• Prevents dilution below fundamental value

5. One-way emission

• Once released, tokens are fully fungible in the pool; there's no "recall"
• System never retracts previously released tokens
• Makes minting supply-monotone and easy to audit on-chain
• Ensures predictable, transparent supply growth

6. Pool primacy

• There is only one market: the CLAMM pool
• All prices, release decisions, and floor checks reference $p_{\text{pool}}$ (guarded)
• No external listing venues or order books influence release dynamics
• Single source of truth for all market activity

7. Acquisition integrity

• Each release curve is bound to a cryptographic record of its acquisition event
• System verifies $p^{\text{acq}}$ once at minting; it remains immutable thereafter
• $p^{\text{acq}}$ acts as a hard lower bound for any protocol-initiated sale
• On-chain attestation prevents acquisition price manipulation

8. Causality (market-follows, never leads)

• Release curve reacts to market conditions; it never predicts or leads them
• All price motion that drives release decisions must originate from trades in the pool
• System is purely reactive, ensuring fair price discovery
• No front-running or anticipatory supply dumps

Mathematical summary

$$\boxed{ \begin{aligned} & p_{\text{guard}}(t) \geq p_{\text{pool}}(t) \\ & p_{\min}(u) = \max(p^{\text{acq}}, p_{\text{guard}}(t_0 + u)) \\ & p_{\text{pool}}(t) \geq p_{\min}(u) \Rightarrow \text{release at pool price} \\ & p_{\text{pool}}(t) < p_{\min}(u) \Rightarrow \text{release at floor price } p_{\min}(u) \\ & m_{\text{released}}(u) = \alpha m (u/\tau)^{\gamma_q}, \text{ monotone, convex} \\ & \text{Tokens never sold below } p^{\text{acq}} \text{ (acquisition cost)} \end{aligned} }$$

Intuitive summary

• Never sell below acquisition cost
• Never release faster than the market can absorb (convex quota)
• Always release at fair price (pool price if above floor, floor price if below)
• Provide natural price support (limit orders at acquisition cost when market dips)
• Only one market: the pool itself
• All releases are reactive, not proactive

Together these invariants make the release curve a market-synchronized, one-way, price-protected supply valve — mathematically simple, economically strict, and self-contained within the CLAMM.

---

Governance guardrails

• Depth clamp: $p_{\min}(u) \geq \text{RWAP}_Q(u)$ — never release below depth-aware average.
• Floor enforcement: If $p_{\text{pool}} < p_{\min}(u)$, tokens can only be sold at $p_{\min}(u)$ via limit orders; no market sales below floor.
• Router enforcement: Any attempt to sell mint tokens below $p_{\min}(u)$ reverts on-chain.
• Issuer bond: Slashed if issuer attempts to sell below $p_{\min}(u)$ or misrepresents acquisition price.

---

Parameterization

Parameter	Meaning	Typical value
$\tau$	Release horizon	30 days
$\gamma_q$	Quantity-curve convexity	2
$\alpha$	Fraction subject to schedule	0.8

Longer horizons or higher $\gamma$ values suit thin or volatile markets.

---

Trade-offs

Advantages

• Prevents sudden dilution
• Enables orderly price discovery
• Fair access for all participants
• Reduces front-running risk
• Provides natural price support at acquisition cost
• Continuous supply flow even in weak markets

Disadvantages

• Slower full liquidity
• Some capital inefficiency while tokens are locked
• Added operational complexity
• Limit orders may wait for buyers if market drops below floor

---

Conceptual intuition

Think of the release curve as a dynamic price-protected emission valve for the CLAMM:

• When pool price is strong (≥ floor) → tokens flow in at pool price, following market naturally
• When pool price weakens (< floor) → tokens continue to flow, but only via limit orders at floor price, providing buy support
• Over time → quota grows (convex curve), ensuring supply flows gradually rather than all at once
• Always → no token ever sells below acquisition cost, protecting fundamental value

The pool's own pricing logic remains the only market—the release curve just ensures supply enters at fair prices.

---

Related reading

• Price dynamics and risks
• Hold period
• Open interest
• Spot Trading CLAMM pricing

---

Summary

The release curve regulates both time and price of new supply entering the pool. It defines a growing quota of tokens that could be released, and ensures they are sold either at the current pool price (if above the floor) or via limit orders at the floor price (if below), guaranteeing no token ever sells below acquisition cost. This ensures smooth, transparent, and manipulation-resistant issuance that synchronizes with market demand while providing natural price support at fundamental value.